Gradient Wind : Cyclonic Curved Flow (subgeostrophic)

The figure above shows the curved (gradient wind) flow associated with a low pressure center. A curved path means the direction of the parcel is changing, which means the parcel is undergoing acceleration (acceleration is either a change in speed or a change in direction). If the parcel experiences acceleration, then the net force on the parcel is not zero. The net force vector in this case is shown on the figure; it points to the center of the low, which also represents the center of the circular path the parcel is riding. Let $r$ represent the radius of the circular path, and $v$ represent the tangential speed of the parcel. The net force in this case is called the "centripetal" (center-pulling) force, and its magnitude is given as $v^2/r$.

The resulting speed of the parcel in cyclonic flow is less than the speed a parcel would have under the same pressure gradient force (acceleration) in the case of a geostrophic wind. To understand why this is so, we will analyze the various forces at work. To do so, we will set up a circular reference frame to match the motion of the parcel. One dimension is the radial distance from the center of the low outward to the parcel. The other dimension is that given by the tangent direction to the circular path the parcel is moving along.

The first force vector to identify is the pressure gradient. The magnitude per unit mass is given by $\frac{1}{\rho}\frac{\Delta P}{\Delta r}$ and the direction of the force is inward. Because pressure increases with $r$ in this scenario, a minus sign is required to give the correct direction - opposite increasing $r$.

Next, the Coriolis deflection, with magnitude $2\Omega \cdot v \cdot \sin \phi$ points to the right of the instantaneous velocity vector of the parcel. The parcel's velocity vector at any instance points in a direction tangent to the circular path and in a counter-clockwise direction. Consequently, the Coriolis force points "outward" from the center, in the direction of increasing $r$. These two forces are not in balance as they are in the geostrophic case. The centripetal force represents the net force in this case, and it points inward, or in the direction of $-r$. The resulting force vectors give the equation

$ -\frac{1}{\rho}\frac{\Delta P}{\Delta r} + 2\Omega \cdot v \cdot \sin \phi = -\frac{v^2}{r_0}$
$\Rightarrow$
$2\Omega \cdot v \cdot \sin \phi + \frac{v^2}{r_0} = \frac{1}{\rho}\frac{\Delta P}{\Delta r} $

The second version of the gradient wind equation for cyclonic flow shows why the speed of the gradient wind in this case is less than the speed of geostrophic wind for the same pressure gradient magnitude. In the geostrophic case, the $v^2/r$ term is not there, so if it is removed, the left side of the equation loses a positive quantity. Consequently, the Coriolis term on the left hand side must increase in magnitude for it to balance the constant pressure gradient on the right hand side. The resulting geostrophic wind speed $v_g$ must be greater than the original gradient wind speed denoted by $v$. That is, $v < v_g$.

Gradient Wind : Anticyclonic Curved Flow (supergeostrophic)

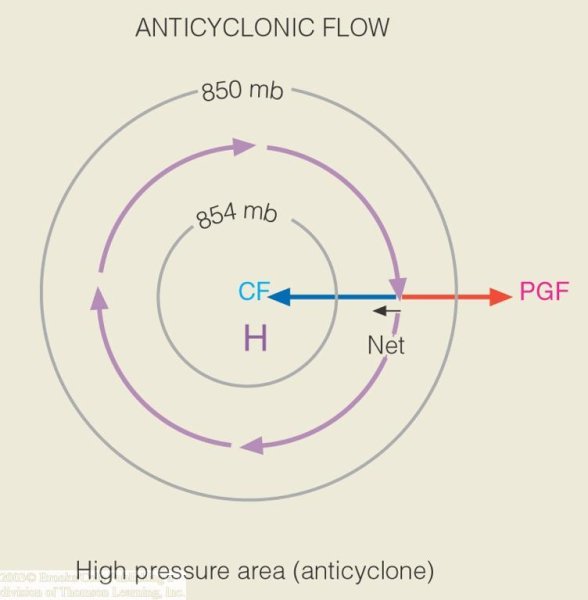The case for anti-cyclonic flow is very similar to that for the cyclonic flow in that all the same forces are in play. However, their respective directions of the pressure gradient and Coriolis forces are opposite those in the case of cyclonic flow. That is, the pressure gradient force points outward from the center and the Coriolis force points inward. The force balance in this case is

$ \frac{1}{\rho}\frac{\Delta P}{\Delta r} - 2\Omega \cdot v \cdot \sin \phi = -\frac{v^2}{r_0}$
$\Rightarrow$
$2\Omega \cdot v \cdot \sin \phi = \frac{1}{\rho}\frac{\Delta P}{\Delta r} + \frac{v^2}{r_0}$

The second form of this equation shows the positive contribution of the centripetal force requires and increase in the geostrophic speed in order for the Coriolis term to balance the original pressure gradient magnitude. This means the anticyclonic gradient wind speed $v$ is greater than the geostrophic wind speed $v_g$ for the same pressure gradient magnitude.

Please note that even though anticyclonic wind speeds are called "super geostrophic," this does not imply that wind speeds associated with high pressure centers or ridges are, generally, greater than those associated with low pressure centers and troughs. The relative winds speeds of anticyclonic, geostrophic, and cyclonic flows are based on pressure gradient force magnitudes that are EQUAL between all three scenarios. In reality, the pressure gradients associated with lows and troughs are GREATER than those associated with highs and centers, so observed cyclonic wind speeds are typically faster than those observed around high pressure centers and ridges.