< Back to Print Version Table of Contents <
Simple Runoff Modeling Methods

At a very basic level, a simple rainfall runoff model could just compute the amount of rain running off a hard surface. An example would be if we looked at a paved parking lot covered with concrete or asphalt. Since no bare ground areas are present, infiltration would not take place. The amount of runoff from the parking lot would be about equal to the amount of rain that fell. Or, stated another way, the input would simply be rainfall and the output would be the runoff.
The Rational Method
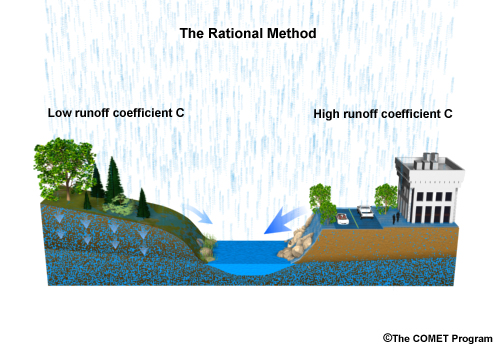
One of the simplest hydrologic situations to model is the peak runoff from a small area (less than 200 acres or 81 hectares). The Rational method estimates only the peak flow using rainfall intensity, area, and a land use factor. Note that using this method, there is no timing associated with the peak flow.
The equation is:
Peak Runoff, Q p = CIA (English units)
Peak Runoff, Q p = CIA/360 (metric units)
C is the land-use runoff coefficient that has no units associated with it, In English units, I is the average rainfall intensity in inches per hour, and A is the area in acres. The peak runoff is in cubic feet per second.
If metric units are used, C doesn’t change. I is the rainfall intensity in millimeters per hour. A is the area in hectares. And a conversion factor of 1/360 is needed to calculate the peak runoff in cubic meters per second.
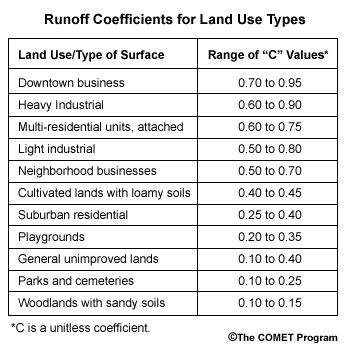
The value of C is found by using a table listing land use types.
The Rational method is used for computing peak runoff from small areas such as parking lots, crop lands, or public parks. It is primarily used in small basins where the coverage of impermeable surfaces is important.
This method provides no robust means of accounting for infiltration.
Complex Hydrologic Models
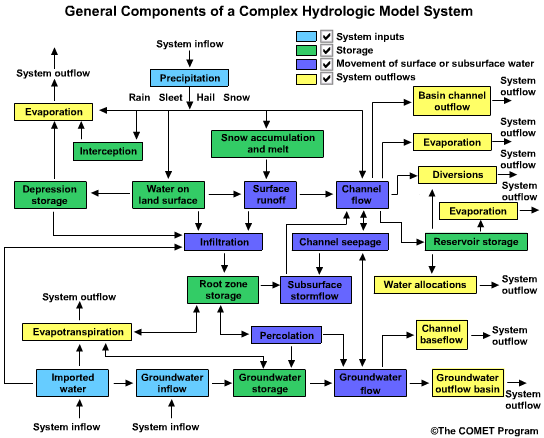
While simple hydrologic models are limited by assumptions and calculations, more complex models allow us to better approximate different parts of the hydrologic cycle. We can see from this diagram that a hydrologic model may take into account a complex array of natural and human-influenced factors.
In this model we see the input and movement of water through an idealized hydrologic system.
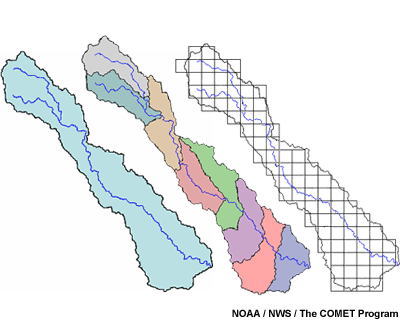
Lumped Modeling
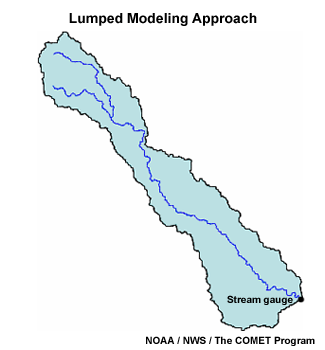
The most basic approach for more complex modeling of runoff from a basin is called the “lumped” method. This type of hydrologic model views a particular drainage area as a single unit and uses basin-averaged hydrologic and meteorological inputs. The output from a lumped model is usually a hydrograph at the basin outlet.
In the past, lumped modeling methods were required due to data collection methods and software limitations. Lumped models are still useful for producing flood guidance. They require less data input and less computational power than more modern methods. However, as new geo-spatial technologies become available, lumped models are being replaced by methods using more detailed spatial information to examine the basin on a finer scale.
Semi-Distributed Modeling
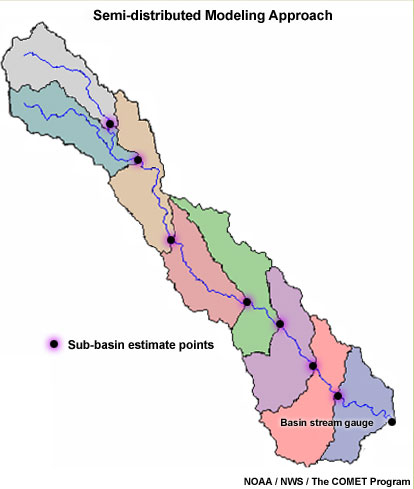
Semi-distributed modeling is a variation of the lumped method and is sometimes referred to as a “pseudo-distributed” approach. Using this approach, a basin is broken down into smaller sub-basins. Runoff amounts from methods such as unit hydrograph are used to estimate streamflow from each of these sub-basins. These runoff volumes are then routed downstream to estimate the streamflow output for the larger basin at the outlet.
Distributed Modeling
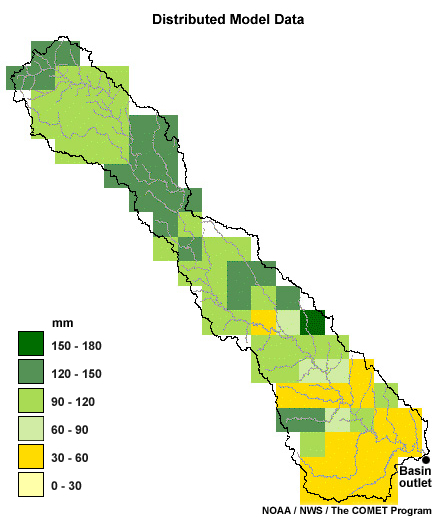
A truly distributed modeling approach is one that represents processes in
a gridded manner and also provides for detailed predictions at the grid-cell
level.
With this type of approach, each cell has parameters allowing for its own streamflow estimates. The flow at any grid point can be estimated mathematically.
One drawback to distributed modeling is the additional input data required for each cell. If these data are not available, they must somehow be estimated, introducing an uncertainty factor.
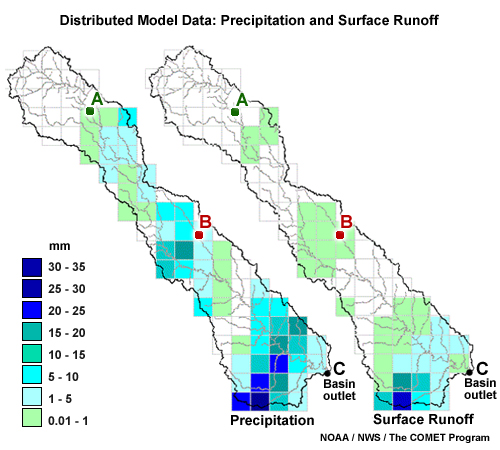
Here we have gridded precipitation and surface runoff data for a basin. Very little rain fell on the upper part of the basin. There is no streamflow response at point A. Small amounts of rain fell in the middle of the basin, so the streamflow does show a small response at point B.
The heaviest rain fell in the lower part of the basin resulting in a significant and rapid peak flow at point C.
A lumped simulation for this basin would only show the averaged effects over the whole basin. It would underestimate the peak amount for point C, and the timing at point C would be inaccurately delayed.
The distributed model, however, is able to capture the spatial variability of the precipitation and produce a more reasonable simulation at point C as well as flow estimates at points A and B.
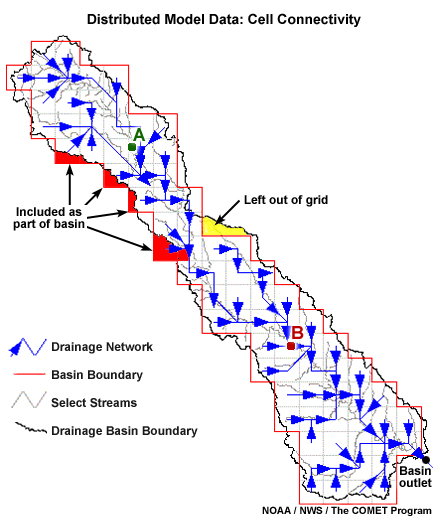
In this image we see the downstream flow vectors for each cell. Physics-based parameters and equations are used to route flows from cell to cell to the outlet.
Keep in mind that this represents an estimate of the flow path. We see that some parts of the basin are left out in the conversion to the grid representation. At the same time, other areas that actually lie outside of the basin are included in the gridded area.
Distributed Modeling Issues
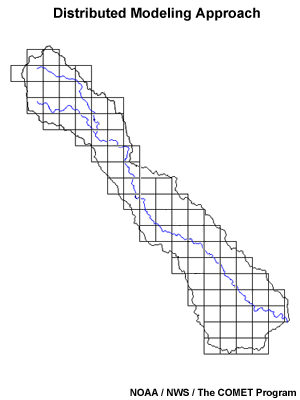
Distributed modeling methods allow modeling of smaller and smaller basins. They also allow computation of more realistic runoff within a basin. Flash flood forecasts, for example, have improved with the implementation of distributed models.
Distributed models do however require more complex and more high-resolution data, introducing more uncertainty.

Distributed hydrologic models are becoming more spatially complex as technologies such as Doppler radar, Global Positioning System (GPS), and Geographic Information Systems (GIS) are used to create geo-referenced, gridded datasets.
In Depth: Types of Models
The term “hydrological model” can have various definitions depending on how a natural system is examined and the complexity involved. Sometimes a particular modeling approach may have more than one name, which can cause confusion.
General definition:
Model – A scaled reproduction of a system, a mental conceptualization, an empirical relationship, or a series of mathematical and statistical equations representing a system. Models are imperfect representations, but are valuable tools with which to study a variety of conditions and predict answers that would be impractical to obtain by measuring or observing the actual system.
Various specific definitions:
Analog model – A model based on similarities between the system under study and another system or process.
Analytical model – A model that uses classic methods such as calculus or algebra to solve a series of equations.
Conceptual model – A simplified representation of the system being examined.
Continuous model – A model that uses continuous simulation, as opposed to a single-event model.
Deterministic model – A model that produces the same output for a given input without consideration for risk or uncertainty.
Empirical model – A model represented by simplified
processes based on observation, measurements, or practical experience rather
than solely on principles or theory. A lumped model is an example.
Explicit model – A numerical model that uses parameter values or unknown variables at the beginning of a time step in the computational algorithms.
Implicit model – A numerical model that uses parameter values or unknown variables at the end of a time step in the computational algorithms.
Mass balance model – A model based on the conservation of mass and focuses on balancing inputs and outputs from the model area. Also known as a zero-dimensional model.
Numerical model – A model that uses a numerical method to solve a series of equations, as opposed to an analytical model. The results from numerical models are often approximations, while analytic models produce exact solutions.
One-dimensional model – A model that includes only one space dimension.
Pseudo-deterministic model – A semi-distributed model.
Stochastic mathematical model – A model that includes statistical elements and produces a set of outputs for a given set of inputs. The output represents a set of expected values.
Two-dimensional model – A model that includes two space dimensions, usually horizontal and vertical averaging.
Review Questions:
1. Lumped models cannot account for details in the rainfall distribution and basin topographic features.
(Choose the best answer.)
a. True
b. False
2. Compared to lumped models, distributed models _____.
(Choose all that apply.)
a) are more computationally intensive
b) are less suited for flash flood situations
c) view the basin as one unit
d) account for details in rainfall and basin characteristics
3. Semi-distributed models may provide more detail about potential runoff than lumped models by _____.
(Choose the best answer.)
a) using the full resolution of gridded rainfall data
b)
averaging the rainfall over the whole basin
c)
estimating runoff for sub-basins within the basin
d)
breaking the basin into grid cells for runoff estimation.
4. The Rational method for estimating runoff uses a land use coefficient, C, which would be ____ for a shopping mall than for a patch of woodland.
(Choose the best answer.)
a) much higher
b) a little higher
c) much lower
d) a little lower
Review Question Feedback
1. Lumped models cannot account for details in the rainfall distribution and basin topographic features.
(Choose the best answer.)
The correct answer is a) True.
2. Compared to lumped models, distributed models _____.
(Choose all that apply.)
The correct answers are a) are more computationally intensive and d) account for details in rainfall and basin characteristics.
3. Semi-distributed models may provide more detail about potential runoff than lumped models by _____.
(Choose the best answer.)
The correct answer is c) estimating runoff for sub-basins within the basin.
4. The Rational method for estimating runoff uses a land use coefficient, C, which would be ____ for a shopping mall than for a patch of woodland.
(Choose the best answer.)
The correct answer is a) much higher.
End of Section Five: Runoff Modeling Concepts