| CLL-SLL Modeling | Spring 2023 | |
| Model Information |
G$_0$ Cell Model. Wikipedia Page
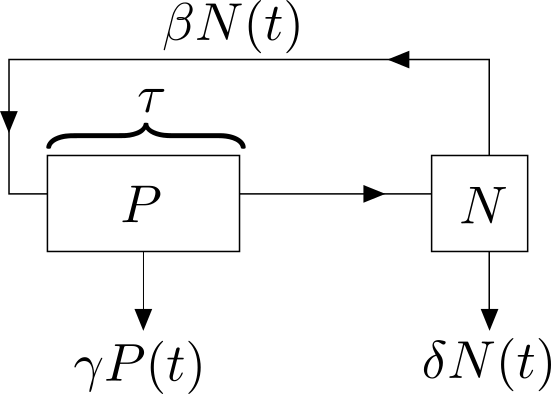
The G$_0$ cell model consists of two cell compartments. One compartment corresponds to cells in a non-proliferation phase ($N$), and the other corresponds to cells in the proliferation phase ($P$).

Model variables and parameters are:
The function $\beta$ plays a "feed back" role and its value is a function of two additional parameters $\theta$ and $n$. The formula for $\beta$ is given as
$$\beta(N) = \beta_{N, 0}\frac{\theta^n}{\theta^n + N^n}$$
where $\beta_{N, 0}$ is the maximum recruitment rate. For a fixed value of $\theta$, as the value of $N$ (the numer of CLL in non-proliferation stage) increases, the value of $\beta$ decreases. The shape (or rate) of decrease is affected by the value of $n$. As the value of $N$ goes to zero, the value of $\beta$ approached unity.
Consequently, there are two population variables, $N$ and $P$, the function $\beta$ that depends on the population $N$, and six parameters, $\beta_{N,0}, \theta, n, , \tau, \gamma, $, and $\delta$.
The dynamics of the G0 model are modeled using the two-equation system of time-delay ODEs. \begin{align} \frac{dN}{dt} &= -\delta N(t) - \beta(N(t))N(t) + 2\beta(N(t-\tau))N(t-\tau)e^{-\gamma \tau} \\ \frac{dP}{dt} &= -\gamma P(t) + \beta(N(t))N(t) - \beta(N(t-\tau))N(t-\tau)e^{-\gamma \tau} \end{align}
In the equations above $N(t-\tau)$, represents the time-delay feature of the cell cycle model.
Qualitative analysis of the G$_0$ Model.
The two equation model has $N$ changing independently for $P$, whereas $P$ depends on $N$. Consequently, the condition for a steady-state (equilibrium) solution for $N$ can be determined independently from $P$. At steady state, $N(t) = N(t-\tau)$ and $dN/dt = 0$, so the ODE for $N$ above becomes
\begin{align}
0 &= -\delta N - \beta(N) N + 2e^{-\gamma \tau}\beta(N)N \\
0 &= -[\beta(N) + \delta]N + 2e^{-\gamma \tau}\beta(N)N \\
0 &= N \left[ -[\beta(N) + \delta] + 2e^{-\gamma \tau}\beta(N) \right] \\
\end{align}
A non-trivial solution requires $N \neq 0$
\begin{align}
0 &= -[\beta(N) + \delta] + 2e^{-\gamma \tau}\beta (N)\\
\beta(N) + \delta &= 2e^{-\gamma \tau}\beta (N)\\
2e^{\gamma \tau}\beta (N) - \beta(N) &= \delta \\
\beta (N) [2e^{\gamma \tau} - 1] &= \delta \\
\beta (N) &= \frac{\delta}{2e^{\gamma \tau} + 1} \\
\beta _0 \frac{\theta ^n}{\theta^n + N^n} &= \frac{\delta}{2e^{\gamma \tau} + 1} \\
\beta _0 \frac{1}{1 + \left( \frac{\theta}{N}\right)^n} &= \frac{\delta}{2e^{\gamma \tau} + 1} \\
1 + \left( \frac{N}{\theta}\right)^n &= \beta_0\left[\frac{2e^{-\gamma \tau} - 1}{\delta} \right]\\
N &= \theta \left[\frac{\beta_0}{\delta} \left[2e^{-\gamma \tau} - 1 \right] - 1 \right]^{1/n}
\end{align}
G$_0$ Cell Model Stability Analysis(Makey and Mackey & Andersen). Long Period Oscillations in a G$_0$ Model of Hematopoietic Stem Cells
CLL Models
The Savvopoulos CLL model is a three compartment model where each compartment (bone marrow, blood, and lymph node) incorporates a G$_0$ cell model. (Source: Savvopoulos-S-2019-PhD-Thesis, page 98). One for the bone marrow, one for peripheral blood, and one for the lymph node system including the spleen. Each compartment has its own G0 cell model to simulate the cell non-proliferation and proliferation phases within each general compartment. The parameters $\beta$, $\tau$, $\gamma$, and $\delta$ have values specific to their given compartment.
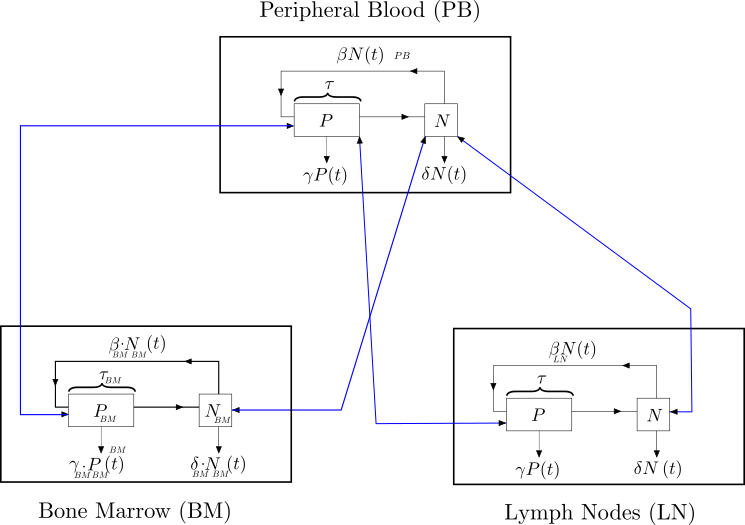
Each of the three compartments have two time-dependent variables and four parameters whose vales are, generally, unique from each other.
Wodarz, et. al Model is a system of two ODEs, one for the CLL cells in lymph tissue and one for peripheral blood. Article \begin{align} \frac{dx}{dt} &= -mx - d_1(x-c) \\ \frac{dy}{dt} &= mx - d_2y \end{align}
Initial conditions (quatifying initial volumes of CLL cells in each compartment.)
Parameter values, methods, ranges
| Parameter | Nominal | Minimum | Maximum |
|---|---|---|---|
| $\beta_0$ (days$^{-1}$) | 3.350 | 1.690 | 5.070 |
| $\delta$ (days$^{-1}$) | 0.001 | 0.001 | 0.020 |
| $\gamma$ (days$^{-1}$) | 0.706 | 0.530 | 0.866 |
| $\tau$ (days) | 0.792 | 0.625 | 0.792 |
| $\theta$ ($\times 10^{8}$) | 0.279 | 0.154 | 6.209 |